I’d like to cut a rectangle into a 3×4 grid of squares. To minimise the number of cuts, should I cut three long strips first, or four short strips? Does it matter?
Here’s the talk I gave at this year’s Big MathsJam Gathering. I called it Please don’t overthink this (I already have)
That’s the short version of the story. I really did spend a lot of time thinking about this!
Recently I presented a maths workshop for some year 3/4 kids in a local school. For those outside England and Wales, that means kids aged 7 to 9.
My plan was to talk about fractions by making up patterns from paper squares of different colours.
In order to do this, I needed lots of paper squares. The school aren’t providing any material themselves (or paying for my time…) so I want to do this on the cheap. So I’ve ruled out just buying lots of origami paper.
I ordered a ream of red A4 paper and pinched a ream of white A4 from my department’s resource room.
So I have to decide how to cut A4 sheets, which are silver rectangles, into squares.
A sheet of A4 paper measures 210×297mm.
The most obvious way that occurred to me was to cut a strip off the long side to end up with a 210mm square, and then halve that in each direction until I get squares of a suitable size. I thought that halving once would give me 105mm squares, which feel about the right size.
But the 87×210mm strip left over felt too big to me.
Then I realised that 210 is 3×70, and 297 is only a little bit more than 280 = 4×70, so I could get 12 70mm squares out of each sheet, only leaving a little strip.
This feels like the most efficient use of the material.
While I was in my office pondering this, my colleague Shweta popped her head in. As I tried different options out, I talked about the practical aspects of cutting up paper.
I know how to fold a rectangle to get the biggest single square, and I think that doing a clean rip along a folded line is one of life’s most sublime experiences.
To subdivide this square, I could fold and rip again. I’d been having a fairly gloomy day, but this cheered me up.
While this method is satisfying, it’s not quick. It was clear that I’d need to use the guillotine in the resource room.
I wondered about how to accurately cut to the right size using the guillotine. Folding to mark a line, as well as being slow, would make it harder to put the paper through the guillotine.
While still in my office, I concluded I’d need to make a template square of the right size by folding, and use that to determine how far to push the paper through the guillotine.
When I got down to the resource room, of course, I saw that the guillotine has a ruler marked on it.

Because I’d decided on 70mm squares, a nice round number, I could line my paper up exactly with one of the marked lines.
But when I started with my first sheet, I spent longer than I like to admit staring at the ruler and trying to work out how to trim off the 17mm from the end. The 17mm mark is under the plastic guard that stops you cutting your fingers off, and the lines are only 5mm apart so it’d be tricky to reliably hit it.
The realisation that hit me was the first time commutativity of operations came into play that day. The second came right at the end.
It’s obvious now that trimming at the 17mm mark, leaving you with pieces 17mm and 280mm long, is equivalent to trimming 280mm, leaving you with pieces 280mm and 17mm long.

So this is my algorithm for cutting the squares I want:
- Push the paper through, portrait, until the bottom edge is on the 280mm mark, and slice.
- Then push through and slice at the 210, 140, and 70mm marks. Even though this is only three cuts, it leaves you with four 70×210mm strips. This was the first appearance of a fencepost error.
- Then turn the strips round and push them through, cutting at the 140 and 70mm marks. This leaves you with three 70mm squares for each strip.
After doing that for a while, I started to wonder: does it matter if I do the horizontal cuts before the vertical ones? Could I save myself a cut or two?
I tried both ways but wasn’t sure I’d counted the cuts properly. I needed to prove how many cuts it takes with each method. And is there an even quicker method that will reveal itself?
I started seeing an algebraic structure: think about the multiset of pieces of paper that I have. I begin with a single $(4,3)$ piece. The two moves I can make are to cut a piece $(a+b, c)$ into two smaller pieces $(a,c)$ and $(b,c)$, or to cut a piece $(a,b+c)$ into two pieces $(a,b)$ and $(a,c)$. For example, $(4,3) \to (3,3) + (1,3)$.
All I have to do is either prove or find some theorems about this system and I can work out the quickest route from $1 \times (4,3)$ to $12 \times (1,1)$.
I can make vertical or horizontal cuts, so it should be fairly simple to draw out the Cayley graph of this thing and find the shortest path in it…
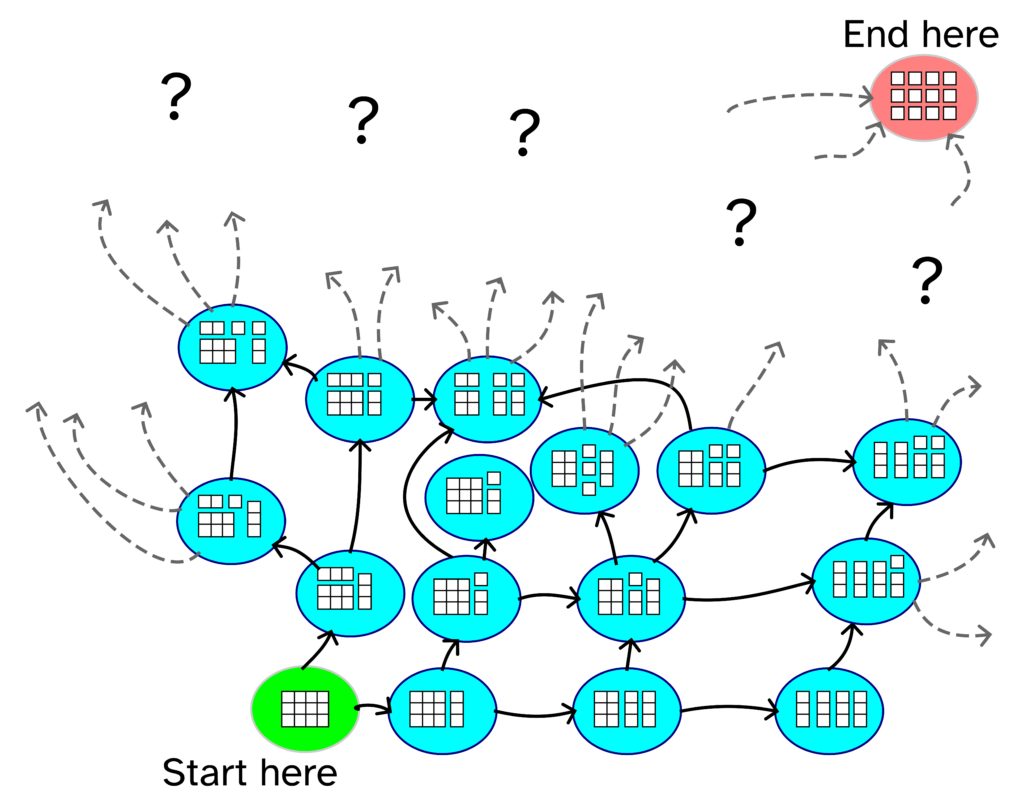
The problem is that at each stage, you haven’t just got two possible moves – horizontal or vertical – you’ve got at least as many moves as different shapes, and some shapes can be cut in a few different ways.
Bonus question: what’s the most different shapes you can have at one point in time? Is it in that picture?
What you need to know about me is that I started a PhD in group theory and then gave up on it. I like abstract algebra in the abstract, but I don’t like actually doing it. I can’t tell from that half-a-diagram where the symmetry is, and I don’t think I’d be able to see it even if I drew the whole thing out.
I was thinking through all this as I was guillotining paper. I tried doing all the vertical cuts first, and then I tried doing all the horizontal cuts first. I wasn’t really keeping count of the number of cuts, because I was also trying to keep track of how much paper I was using. (I ended up making about two thousand squares too many)
Eventually, I realised something that makes the solution completely obvious:
- Each time I make a cut, I have one more piece than I used to.
- I start with one piece.
- I want to end up with twelve pieces.
So it doesn’t matter what I do or in what order: it’ll always take 11 cuts.

That’s really simple! A child could understand it! You could understand it! I could understand it!
But imagine if I hadn’t told you about all the thinking I’d done to get there?


