By Tori Cole, Specialist, IM Certified Facilitator
Timesha Brooks, Specialist, Math Client Support
Engaging Reluctant Math Students
Have you encountered students who are reluctant to engage in math? Students who have already decided they are “bad” at math? How do we support students whose mathematical identities seem fixed before they even enter our classrooms?
As a middle school teacher in a large urban district, I faced these challenges head-on. My seventh-grade classroom was filled with students who didn’t see themselves as “good” students and who lacked enthusiasm due to limited access to powerful mathematics practices. My goal was to create a space where they could see themselves as capable and confident mathematicians.
Transforming these identities took time, focus, trust, and intentionality. By leaning into warm-up instructional routines and creating space for collaboration, students built on their own thinking by borrowing their peers’ strategies, words, and ideas. Students began arriving to class eager to participate. I observed an openness to unlocking math problems collectively, trying out different strategies, and engaging in mathematical discourse. Gradually, they started reforming their math identities. When asked by parents and administrators, most of these students said math had become their favorite subject.
Building Positive Math Identities
A positive math identity is the perception of oneself as capable and competent in math. It is crucial for lifelong engagement with math and is shaped by personal experiences, social influences, and educational practices. Developing a positive math identity involves cultivating confidence, curiosity, and enjoyment in learning and using mathematics (Aguirre, Julia M., Mayfield-Ingram, Karen, and Martin, Danny B, 2013).
Educators play a critical role in building positive math identities. By creating inclusive, supportive learning environments, employing teaching methods that emphasize understanding and problem-solving, and encouraging collaboration, teachers can help students see math as dynamic and accessible. Celebrating diverse mathematical thinking also contributes to a positive identity, helping students appreciate different approaches and perspectives.
Imagine a world where all learners know, use, and enjoy mathematics! This vision is central to Illustrative Mathematics. One way to turn this vision into a reality is by implementing instructional routines and teaching practices that build positive math identities.
Instructional Routines
Instructional routines are structured, predictable activities used regularly in the classroom to support learning. They provide a stable framework within which students can engage with mathematical concepts, allowing them to take intellectual risks and explore math without fear of failure. Staple IM routines such as daily math warm-ups and lesson activities encourage active participation and reinforce the idea that everyone can contribute to mathematical discussions.
These routines also facilitate the development of a growth mindset by emphasizing effort, persistence, and the learning process over simply getting the right answer. Reflective practices, such as math journals or discussions about different problem-solving strategies, help students value their own thinking and understand that making mistakes is a natural part of learning. Over time, these routines help students believe they can improve their mathematical abilities through practice and perseverance (Boaler, Jo., 2016).
Types of Instructional Routines
Illustrative Mathematics curriculum includes many different instructional routines. Some are used primarily in warm-up routines and others during the lesson activity.
Warm-up Routines
Each lesson begins with a warm-up designed to elicit student discussions about the lesson’s mathematical goal. These routines provide opportunities for students to bring their personal experiences and mathematical knowledge to problems and discussions, placing value on their voices as they communicate ideas, ask questions, justify responses, and critique reasoning.
Warm-up routines serve two purposes:
- To help students get ready for the day’s lesson
- To strengthen number sense or procedural fluency through mental arithmetic or numerical reasoning
One of the more popular warm-ups is Which Three Go Together?. This routine, formerly known as Which One Doesn’t Belong?, was renamed for IM® v.360 as a direct result of feedback from the IM community, which questioned the inclusiveness of the original title. After much conversation, research, and brainstorming, Which Three Go Together? was chosen to celebrate the connections between representations. This was an intentional shift to illustrate the connectedness of a math community and to disrupt the narrative about who belongs in the mathematics classroom.
Which Three Go Together?
This routine presents students with four figures, diagrams, graphs, or expressions and prompts them to decide which three go together. Each group of three go together for different reasons, and students must explain their rationale, fostering precise language use and deeper understanding.
An important aspect of the Which Three Go Together? routine is the idea of looking at characteristics, quantities, or structures that are the same and different, yet having all four items be part of a group. This routine gives students opportunities to identify and name specific characteristics, which help them develop their mathematical language skills.
Here is a Which Three Go Together? example from a Grade 6 Unit 1 lesson.
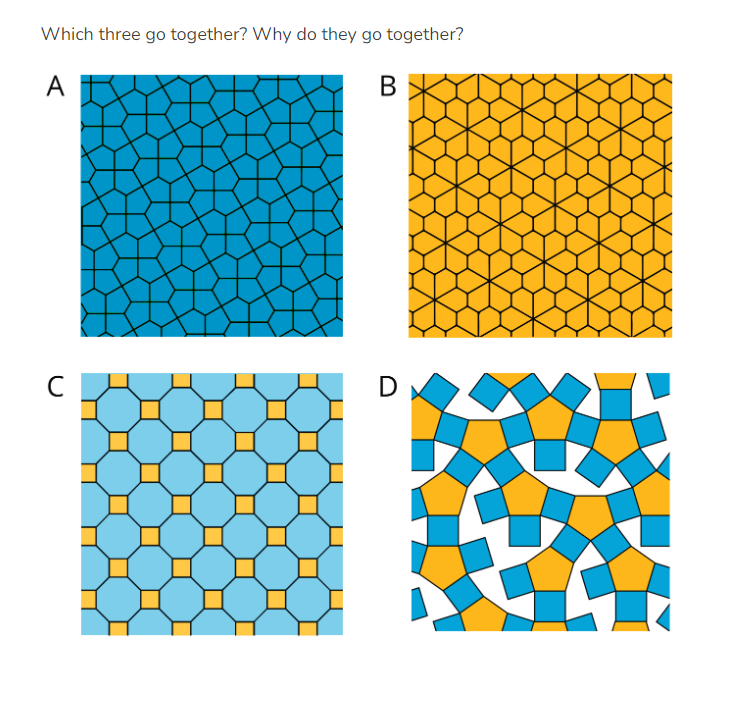
Because this is the first time in the sixth-grade course that students are seeing this routine, they are presented with four representations and asked to determine which three they think belong in a group together. Students individually process which representations should be in a group and then work with a partner to share their reasoning and refine their explanations.
This routine allows for students to look for structure (MP7) and attend to precision (MP6), which helps them better understand connections across representations. Additionally, students are using precise language, because they have to describe geometric characteristics and patterns as they think about how the shapes cover a lane without gaps or overlaps. This further contributes to their understanding of the meaning of area in preparation for the day’s learning activities.
Math Language Routines
Math language routines (MLRs) deepen language and learning while attending to student agency. These routines provide structured yet adaptable formats for amplifying, assessing, and developing students’ language. MLRs support teachers in creating classrooms where students can rebuild their math identities by engaging in meaningful and purposeful interactions.
Picture all the interactions happening in an IM classroom. “Students are expected to say or write mathematical explanations, state assumptions, make conjectures, construct mathematical arguments, and listen and respond to the ideas of others.” This is a lift for all students, especially those students who are multilingual learners, students with disabilities, or students who haven’t had the opportunities to build a strong math identity. “In an effort to advance the mathematics and the language learning of all students, the materials purposefully engage [all] students in sense-making and using language to negotiate meaning with their peers” through structured interactions that are meaningful and purposeful, rather than the focus being on giving or getting correct answers.
Example: MLR 1 Stronger and Clearer Each Time
An example that illustrates how IM v.360 further supports teachers in creating space within their math classrooms for students to build positive math identities comes from Grade 7 Unit 2 Lesson 11, Interpreting Graphs of Proportional Relationships. In previous lessons, students explored the constant of proportionality and agreed on the naming convention of k to represent it. In this activity, students plot data on a graph and are tasked not only with finding k but also with understanding its significance in the given context.
This routine provides a structured opportunity for students to revise and refine their ideas. Through multiple partner meetings and feedback, students revise their understanding, strengthening both their reasoning and math identities.

Here is where Math Language Routine 1: Stronger and Clearer Each Time creates opportunities for students to shine. The task itself could be quickly accomplished: a student answers, maybe discusses with their seat partners, then waits for the Activity Synthesis to hear more and possibly update their thinking. With the integration of Stronger and Clear Each Time (and all MLRs) embedded into the IM® 6–8 Math v.360 curriculum, students will revise their own thinking with multiple peer partners, thereby engaging in productive forms of agency. The teacher’s guide gives the following guidance:
Before the whole-class discussion, give students time to meet with 2–3 partners to share and get feedback on their first draft response to “What does the value of 𝑘 tell you about this context?” (At each partner meeting, students will jot down new words, phrases, or visuals they would like to add to their draft.) Invite listeners to ask questions and give feedback that will help their partner clarify and strengthen their ideas and writing. Give students 3–5 minutes to revise their first draft based on the feedback they receive.
Student Graphic Organizer for Stronger and Clearer Each Time (student sample)

The student’s first idea was their own best thinking about the context of k. But through their journey of partnering with others, asking and answering clarification questions, and building on academic language while attending to precision, students delve deeper into their own mathematical minds, strengthening both their reasoning and their math identities.
Conclusion
The implementation of Illustrative Mathematics’ instructional routines have proven transformative in fostering positive math identities. By providing structured and consistent opportunities for all learners to engage deeply with mathematical concepts, these routines help students see themselves as capable and confident mathematicians. This approach supports diverse learners and creates inclusive environments where all students can develop a strong understanding of mathematical concepts and improve their communication skills.
The strategic use of MLRs has been particularly effective in supporting diverse learners, including multilingual learners and students with disabilities. By creating an inclusive environment where students can express their ideas, ask questions, and receive feedback, MLRs help all students develop a stronger understanding of mathematical concepts and improve their communication skills.
The positive impact of IM’s instructional routines extends beyond individual classrooms, offering a scalable approach that can benefit entire schools and districts. By adopting these routines, educators can ensure that every student has the opportunity to shine in mathematics, fostering a lifelong love for the subject.
Empower Your Students with Engaging Math Practices
As educators, we have the opportunity to shape how our students perceive and engage with mathematics. Illustrative Mathematics’ instructional routines are designed to make math accessible, inclusive, and exciting for all learners. Whether it’s a warm-up routine that sparks curiosity or a math language routine that deepens understanding, these practices have the power to transform your classroom.
Try out one of these routines in your next lesson! Start small—integrate a warm-up routine like Which Three Go Together? or use the Stronger and Clearer Each Time MLR to enhance student discussions. You’ll see how these structured activities not only boost engagement but also help your students develop confidence and a positive math identity.
Take the first step today. Choose a routine, implement it, and watch your students shine in ways you haven’t seen before. As a final thought, use the reflection questions provided in the curriculum when considering how you implemented the instructional routines. Let’s work together to ensure every student has the opportunity to shine in mathematics and foster a lifelong love for the subject.
References:
Aguirre, Julia M., Mayfield-Ingram, Karen, and Martin, Danny B. 2013. The Impact of Identity in K-8 Mathematics: Rethinking Equity-Based Practices. National Council of Teachers of Mathematics
Boaler, J. (2016). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching. Jossey-Bass/Wiley.
 Tori Cole
Tori Cole
Specialist, IM Certified Facilitator
Tori Cole holds a BS in Secondary Education and a MS in Curriculum and Instruction, with a specialization in Supervision. Tori has served as a 6–12 math instructional leader in prominent urban school districts in Miami, Pittsburgh, and Chicago. Tori now works as a specialist at IM, supporting facilitators who bring PL to schools and districts nationwide. She believes that education done well has the power to lift communities.
When not thinking about math education, Tori can be found outdoors in the garden or tending to the family’s backyard chickens.
 Timesha Brooks
Timesha Brooks
Specialist, Math Client Support
Timesha Brooks was born and raised in New Jersey before relocating to Atlanta, Georgia in 1997 to pursue her Bachelor of Science in Mathematics at Spelman College. After graduation, she embarked on a career in education, beginning as a High School Math Teacher in one of Georgia’s largest school districts. Over her 18-year tenure in public education, Timesha earned a Master’s degree in Statistics and an Educational Specialist degree in Educational Leadership, both from Georgia State University. Her diverse experience includes serving as a High School Math Teacher, an International Humanitarian Educator in Osaka, Japan, an Adjunct Professor, an Instructional Coach, and a Math Implementation Specialist for Georgia’s Regional Education Service Agency.
In 2018, Timesha took a bold step in her career by founding IMUnique LLC, an educational consulting company dedicated to empowering teachers and students to realize their mathematical potential. Since then, she has become a sought-after instructional expert, presenter, and trainer, working with educators and leaders nationwide. Timesha is currently the Math Client Support Specialist at Illustrative Mathematics. Outside of her professional achievements, Timesha cherishes her time with her family—her husband of 17 years, Charles Sr., and their two children, Morgan and CJ. Whether they’re tending to horses on their farm, traveling, dining out, or watching movies, family time is her greatest joy.


